Irracionalidad de Raíz de 2:
Demostraremos que Raíz de 2 es irracional, es decir que no se puede expresar como a/b, con b distinto de cero, por Reducción al Absurdo.
Reducción al absurdo: Es un tipo de demostración indirecta: se supone provisionalmente la negación de la tesis y se intenta extraer de esa negación una contradicción. El rechazo de esa contradicción nos indica que nuestra hipótesis provisional es fals
a, por lo tanto la tesis original es verdadera.
Nuestra Tesis:

Supongamos que esta tesis es falsa, es decir supongamos temporalmente que:
Tesis Provisional:
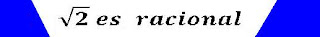
Sabemos que un número racional se puede escribir como una fracción irreductible (que no se puede simplificar más) de 2 números enteros.
Luego:

Elevando al cuadrado:

Reemplazando en (*)

De (1) y (2): M y n son pares, por lo tanto, ambos son múltiplos de 2, o bien ambos son divisibles por 2, lo que contradice nuestra hipótesis provisional de que M/n era fracción irreductible. Entonces la hipótesis de que Raíz de 2 es racional es FALSA.
Por lo tanto Raíz de 2 es irracional.
(Tomado de manual PSU - Matemáticas, Universidad Católica)

No hay comentarios:
Publicar un comentario